TSDT14 Signal Theory
TSDT14 Signal Theory is a course in signal processing, dealing with both time-continuous and time-discrete signals, that are both deterministic and stochastic. The focus is on stochastic signals. The signal processing systems are usually linear and time-invariant, but we also consider some momentary non-linear systems. One part of the course deals with multi-dimensional processes, where we concentrate on two-dimensional processes. We also consider traditional analog modulation methods and perform noise analysis of them. We are especially interested in transformations between time-continuous and time-discrete signals. A smaller part of the course is estimation of power spectral densities using Fourier methods, where DFT is used. Signal Theory is a basis for further studies in signal processing, e.g. Tele(data)-communication, image processing, automatic control, et. cetera.
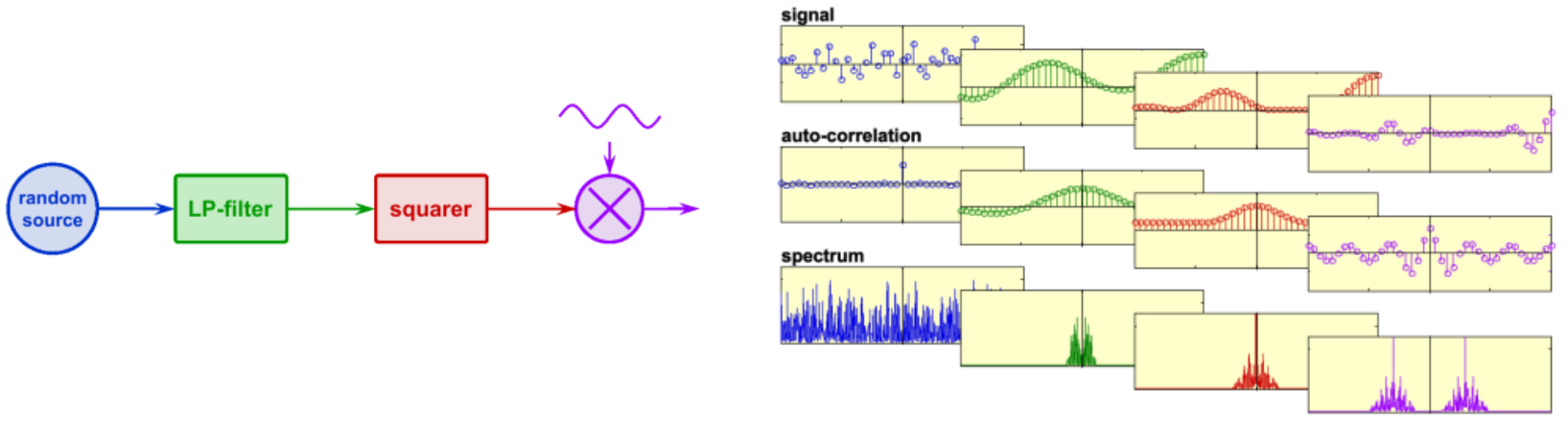
Course topics
-
Time continuous and time discrete, real as well as complex, stochastic processes: Probability distribution, probability density, expectation, ensemble expectation, auto correlation function, power spectral density, cross correlation function, cross spectral density, stationarity, ergodicity. Especially Gaussian processes and white processes. Multidimensional processes.
-
LTI filtering of stochastic processes: Relations between statistical properties of the input process and the output process. Especially matched filters and white Gaussian noise as input.
-
Amplitude and angle modulation of stochastic processes: Relations between statistical properties of the input process and the output process. Especially Gaussian processes as input. Noise analysis of those modulation forms, primarily with white Gaussian noise as disturbance.
-
Non-linear momentary systems: Quantization and monomial non-linearities. Relations between statistical properties of the input process and the output process. Especially Gaussian processes as input. Properties of quantization noise.
-
Transformation between time continuous and time discrete stochastic processes: Sampling and pulse amplitude modulation, the sampling theorem, reconstruction and reconstruction error.
-
Case study: Reconstruction in CD players.
-
Estimation of expectations, auto correlation function and power spectral density.
Instructors
- Course director and lecturer: Danyo Danev
- Teaching assistants: Chung-Hsuan Hu, Ahmet Kaplan
Course material
- The course is based on the book:
- Mikael Olofsson, Signal Theory, Studentlitteratur, 2011.
- Supplementary material:
- Mikael Olofsson, Tables and Formulas for Signal Theory, Studentlitteratur, 2011.
- Lab Memo: Mikael Olofsson, Time-Discrete Stochastic Signals, August 2017.
- Additional lab material: Mikael Olofsson, Short Matlab Manual, August 2017.
- Mikael Olofsson, Signal Theory – Additional Material on Complex Signals.
Prerequisites
- From Calculus: Derivatives and integrals.
- From Probability theory: Most, but with focus on binary distributions, rectangular distributions and Gaussian distributions.
- From Signals and systems or Linear Systems: Fourier transforms, LTI systems, convolution, amplitude modulation, sampling and pulse amplitude modulation. (all of it deterministic)
Information for enrolled students
For detailed lecture, tutorial and lab plans, see the course room in